Metric Spaces¶

A surface is more than just a set of points. Points on a surface have a notion of closeness that doesn’t exist with a set unless we add some structure.

One way we can introduce the idea of closeness is to introduce the idea of the distance between points. That is, a function 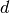$d$ that gives us a number for any pair of points.

To be a distance function, our function must meet some additional requirements:

all distances must be non-negative: $d(x,y)>=0$
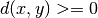
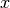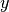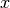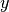the distance between $x$ and $y$ is zero if and only if $x$ and $y$ are the same point: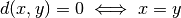 $d(x,y)=0 \iff x=y$
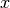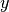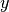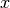the distance between $x$ and $y$ is the same as the distance between $y$ and $x$ . In other words, the distance function is always symmetric: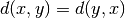 $d(x,y)=d(y,x)$
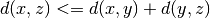
finally, the distance between two points can never exceed the sum of the distance between each of the points and a third point. This is often referred to as the triangle rule: $d(x,z)<=d(x,y)+d(y,z)$

A distance function is often called a metric. A set of points with a distance function is called a metric space.

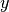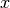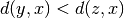A metric space clearly has a notion of closeness. A point $y$ is closer to $x$ than $z$ is if $d(y,x)<d(z,x)$ .